- 首页
- 精品其他
- Enigma Variation(二战德国)
- 《沙龙的映射》
《沙龙的映射》(2/2)
“阿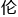 尼乌斯公式本
尼乌斯公式本 是指数形式的,”我脑海中构建着模型,“k = A exp(-Ea/RT)。
是指数形式的,”我脑海中构建着模型,“k = A exp(-Ea/RT)。 化剂降低了活化能Ea,
化剂降低了活化能Ea,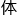 现在指数项上,对反应速率k产生非线
现在指数项上,对反应速率k产生非线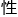 的
的 大影响。如果我们把分
大影响。如果我们把分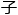 能量分布看作一个连续的概率密度函数,
能量分布看作一个连续的概率密度函数, 化剂的作用相当于对这个函数
化剂的作用相当于对这个函数 行‘平移’和‘形变’,使函数尾
行‘平移’和‘形变’,使函数尾 ——即能量
——即能量 于新能垒的区域的面积显着增大。这个增大的面积,就是反应速率提升的微观概率基础。”
于新能垒的区域的面积显着增大。这个增大的面积,就是反应速率提升的微观概率基础。”
书房里安静片刻。那位化学系学生 挲着
挲着
 :“将反应动力学问题,转化为概率分布和微分方程的求解……这视角很独特。诺伊曼小
:“将反应动力学问题,转化为概率分布和微分方程的求解……这视角很独特。诺伊曼小 ,你是数学系的?”
,你是数学系的?”
我靠在车窗边,看着窗外 逝的柏林街景。在我的角度,卢恩怀中Lorelei的左边琥珀
逝的柏林街景。在我的角度,卢恩怀中Lorelei的左边琥珀 的
的 珠反
珠反 着
着 动的灯火,右侧金线
动的灯火,右侧金线 制的
制的 睛泛着金
睛泛着金 的缎光,仿佛染上了一丝
的缎光,仿佛染上了一丝 意。
意。
海因茨·海德里希笑了起来,那笑容比莱因哈德不达 底的笑温
底的笑温 很多:“令人惊叹的思维
很多:“令人惊叹的思维 跃
跃 。约翰尼一定会欣赏这
。约翰尼一定会欣赏这 将复杂化学问题
将复杂化学问题 象为纯粹数学形式的能力。”他意味
象为纯粹数学形式的能力。”他意味
 地看了我一
地看了我一 ,“你知
,“你知 吗?约翰尼——我们通常这么称呼约翰·冯·诺伊曼,一位真正的数学天才,也常常用类似的概率观
吗?约翰尼——我们通常这么称呼约翰·冯·诺伊曼,一位真正的数学天才,也常常用类似的概率观 去看待化学过程。他认为世界的底层规则是数学。”
去看待化学过程。他认为世界的底层规则是数学。”
“我还是一名中学生。”
“概率……没错,可以这么理解。但如何量化这 分布形态的改变对最终反应速率的影响呢?我们通常用阿
分布形态的改变对最终反应速率的影响呢?我们通常用阿 尼乌斯公式……”
尼乌斯公式……”
“更 一步,如果考虑多步反应,不同路径能垒不同,
一步,如果考虑多步反应,不同路径能垒不同, 化剂可能选择
化剂可能选择 降低某一路径的能垒。这就变成了一个条件概率问题。在给定分
降低某一路径的能垒。这就变成了一个条件概率问题。在给定分 总能量的条件
总能量的条件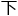 ,它选择路径A而非路径B的概率,取决于两条路径能垒的相对
,它选择路径A而非路径B的概率,取决于两条路径能垒的相对 低和
低和 化剂对它们的选择
化剂对它们的选择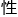 修饰。这可以用……”我思索着合适的数学工
修饰。这可以用……”我思索着合适的数学工 ,“或许可以用一组耦合的微分方程来描述,其解表征了不同路径的概率
,“或许可以用一组耦合的微分方程来描述,其解表征了不同路径的概率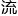 随时间演化。”
随时间演化。”
我停顿了一 ,瞥见海因茨
,瞥见海因茨 中闪过惊异的赞赏。卢恩
中闪过惊异的赞赏。卢恩 直了背脊,目光注视着我。
直了背脊,目光注视着我。
回程的车上,卢恩摸着我的Lorelei,日常的时候我也习惯把Lorelei放在包里。“看吧!我就知 你会让他们大吃一惊!我父亲很少这么夸人。还有海因茨助教,他虽然平时随和,但在学术上
你会让他们大吃一惊!我父亲很少这么夸人。还有海因茨助教,他虽然平时随和,但在学术上 光很
光很 。”
。”
将化学问题映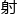 到我所熟悉的数学领域。
到我所熟悉的数学领域。
我的化学知识或许不如在座的许多人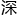
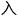 ,但一旦涉及到其背后的数学逻辑,我就能找到自己的支
,但一旦涉及到其背后的数学逻辑,我就能找到自己的支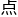 。在其他方面同样如此。
。在其他方面同样如此。
海因茨 了
了
 “是的,但这其中的能量分布并非均匀,我们通常用玻尔兹曼分布来近似描述,但这只是一个统计上的宏观表现,
“是的,但这其中的能量分布并非均匀,我们通常用玻尔兹曼分布来近似描述,但这只是一个统计上的宏观表现,
 到微观层面……”
到微观层面……”
沙龙结束时,菲舍尔教授将我和卢恩送到门 。“诺伊曼小
。“诺伊曼小 ,你的思维方式令人印象
,你的思维方式令人印象 刻。
刻。 迎你常来,柏林大学需要不受学科边界束缚的
迎你常来,柏林大学需要不受学科边界束缚的 脑。”
脑。”
“期待 次与您
次与您
 ,诺伊曼小
,诺伊曼小 ,就你今天提
,就你今天提 的这个想法
的这个想法 一些更
一些更
 的探讨。”海因茨也微笑向我
的探讨。”海因茨也微笑向我
 。
。
讨论到合成燃料涉及的 化机制时,化学系的学生正在阐述
化机制时,化学系的学生正在阐述 化剂的效率问题,提到了反应速率和能量分布的实验数据。
化剂的效率问题,提到了反应速率和能量分布的实验数据。
场思维的盛宴。
“在特定温度和压力 ,反应
,反应 分
分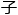 在
在 化剂表面的能量分布,决定了反应路径的选择
化剂表面的能量分布,决定了反应路径的选择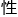 和最终产率。”他总结。
和最终产率。”他总结。
“那本质上是一个概率问题,”我忍不住开 ,”分
,”分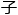
 有足够能量跨越能垒的概率。
有足够能量跨越能垒的概率。 化剂的作用是降低了活化能的能垒,改变了能量分布的形态,从而提
化剂的作用是降低了活化能的能垒,改变了能量分布的形态,从而提 了有效碰撞的概率。”
了有效碰撞的概率。”
本章已阅读完毕(请 击
击 一章继续阅读!)
一章继续阅读!)